
Carsten
Sinz
WelcomeProjects
Publications
Activities
Talks
Software
CV
Links
Projects
Powerful Proof Systems for Propositional Logic
Propositional logic decision procedures lie at the heart of many applications in hard- and software verification, artificial intelligence and automatic theorem proving. In many practical applications it is not sufficient, however, to obtain a yes/no answer from the decision procedure. Either a model, representing a sample solution, or a justification (i.e. a proof), why the formula possesses none, is required. In this project we are investigating the use of powerful proof systems (e.g. Extended Resolution) as a unifying means to compactly and concisely represent propositional logic proofs obtained from the application of different Boolean logic algorithms (e.g. DPLL, BDDs).
SAT Visualization
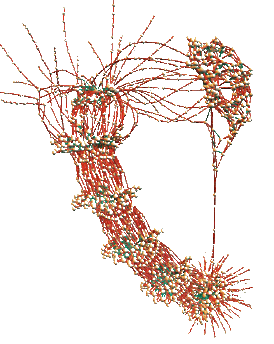 A particular instance of the SAT problem can be considerably easier to
solve than known worst-case bounds would suggest. This is frequently
attributed to the internal structure of the instance. However,
there is no clear understanding on how this structure manifests itself.
As a first step to obtain a deeper understanding we
developed DPvis, a tool that uses
established graph layout techniques (force-directed placement)
to visualize the internal structure
of a SAT instance.
We have also implemented an extension of DPvis that allows
computation of three dimensional layouts.
A particular instance of the SAT problem can be considerably easier to
solve than known worst-case bounds would suggest. This is frequently
attributed to the internal structure of the instance. However,
there is no clear understanding on how this structure manifests itself.
As a first step to obtain a deeper understanding we
developed DPvis, a tool that uses
established graph layout techniques (force-directed placement)
to visualize the internal structure
of a SAT instance.
We have also implemented an extension of DPvis that allows
computation of three dimensional layouts.
Parallel SAT-Solving
SAT solving (as needed, e.g., for Bounded Model Checking) requires huge amounts of computational resources. To speed up the solving process, we developed the parallel and distributed SAT-solver PaSAT. It runs on heterogeneous clusters of (multi-processor) PCs and dynamically distributes work among the available processors. PaSAT is based on the Distributed Objected-Oriented Thread System (DOTS) developed by Wolfgang Blochinger (University Tübingen).
Product Configuration
Products are growing to be individually adaptable to each customer's need. Combining individual configuration with mass production results in a process called mass customization, which puts considerable challenges on companies and their engineering, production, sales and after-sales departments. Special data bases (Product Documentation Management Systems) are employed to capture necessary product knowledge. The knowledge is typically stored in a rule-base using a formal language to express configuration constraints. Rule development, debugging and modification—as software development in general—can be time-consuming and error-prone. To facilitate rule development we applied automated theorem proving methods like SAT-Solving or BDDs to debug configuration data bases by formally proving properties of the data base as a whole. In particular, we applied this methodology to detect residual errors in a rule-base used by DaimlerChrysler to configure their Mercedes cars and trucks. In another project with Siemens Medical Solutions we check consistency and completeness of individually manufactured product manuals.
Verification of Rule-Based Expert Systems
IBM's System Automation® (SA) application is used to automatically manage large applications running on Mainframes and Linux-clusters, possibly consisting of many sub-applications with complicated dependencies. So, e.g., to start an application or move it from one computer to another (e.g. for maintenance reasons), a long sequence of operations involving many sub-systems like data bases may be required. To facilitate this process, SA generates action sequences automatically based on high-level automation goals (e.g. “move application A from computer C1 to computer C2”). In this project, we formalized the rule-based expert system running at the heart of SA as well as SA's execution algorithm (using Propositional Dynamic Logic, PDL) in order to find residual errors (non-terminating computations, loops) in the expert system.